Tag: Python Classes

Circular Buffer in Python

Circular Buffer in Python

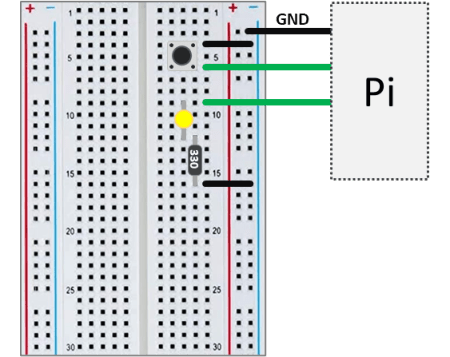
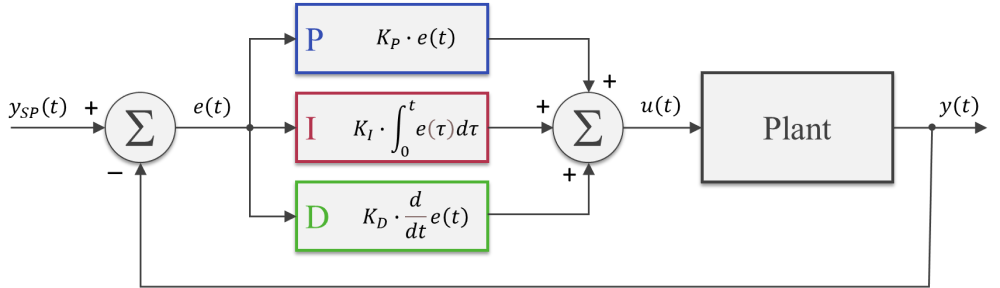
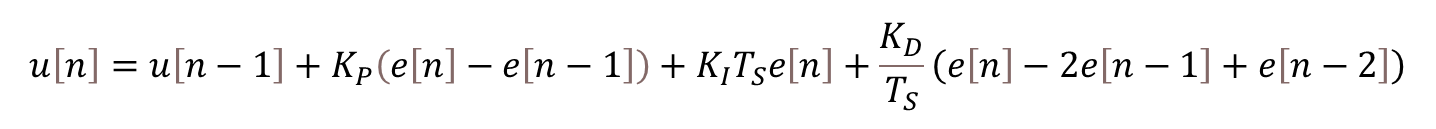A circular or ring buffer is a fixed-size data structure that is commonly used in real-time software applications to store a pre-defined number of values. The analogy of a ring with a fixed number of positions is quite useful to capture the FIFO (First-In-First-Out) nature of such data structure. Once the buffer is full, the first element that was written (“In” ) to the buffer is the first one to be overwritten (“Out”) by the next incoming element.

Circular buffers are particularly useful in situations where the data is continuously being sampled and calculations need to be done using a pre-defined sample size or continuous visualization is required.

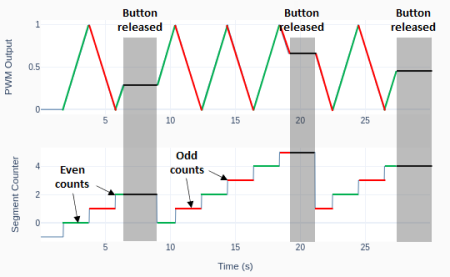
The two images below represent a circular buffer with 10 positions. On the left, with four elements written to it being 5 the “first in”. On the right, the buffer is full where the value 3 was written. Note how the current write position pointer moves around as new values are added.

Additionally, a ring buffer has basically two states: not-yet- full (left image) and full (right image). The not-yet-full state occurs after the buffer is initialized and exists only until it becomes full. We will see later how this affects the Python code used to represent the buffer.

Once the buffer state changes to full, the FIFO nature of this type of data structure becomes evident. In the next two images, the next element “in” is the value 12, replacing the “first in” value 5, which therefore is the “first out”. The next value “in” is 2, replacing the “second in” value 10, and so on.

In the example figures above, we could imagine the buffer being used to display the average value of its elements (once the buffer reaches the full state). As time progresses, a new sample is written to the buffer, replacing the oldest sample. Each figure of the full buffer is a snapshot at a given time step of the sampling process. In this case the average values are 6.4, 7.1, and 6.3.

Python Implementation

The most elegant way to implement the circular buffer is by using a class. Also, a true circular buffer does not involve shifting its elements to implement the FIFO structure. The current position pointer is used to keep track of where the newest element is.

The circular buffer class should have the following attributes:

  • bufsize: the number of elements that the circular buffer can hold (integer)
  • data: the list of elements, i.e., the buffer itself
  • currpos: the current position pointer (integer)

The class should also have two methods:

  • add(): writes an element to the buffer
  • get(): returns a list containing the buffer elements

Let’s go over some of the features of the Python implementation below:

  • As mentioned earlier, the ring buffer has two states (not-yet-full and full). The first state only exists for a limited time until the buffer is filled up. With that in mind, it makes sense to define the __Full class within the RingBuffer class with the exact same methods. Once the buffer is full, the original class is permanently changed to the full class implementation, with its add() and get() methods now superseding the original ones.
  • The not-yet-full add() method just does a regular list append operation of new elements to the buffer list. It is also in this method that the class is changed to the __Full class once the buffer reaches its capacity.
  • The full add() method, on the other hand, writes the new element at the current (newest) element position and increments the current position by one unit (wrapping it around, or resetting it, once the buffer size value is reached).
  • More interesting however is the full get() method. It splits the data list at the current position into two lists which are then concatenated. The list going from currpos to the last element goes first, then comes the list from the first element to currpos (excluded). By returning this concatenated list, the method fully implements the circular buffer without shifting any of it elements! Inspect the data attribute as you add elements to a full buffer to see what the original list looks like.
class RingBuffer:
    """ Class that implements a not-yet-full buffer. """
    def __init__(self, bufsize):
        self.bufsize = bufsize
        self.data = []

    class __Full:
        """ Class that implements a full buffer. """
        def add(self, x):
            """ Add an element overwriting the oldest one. """
            self.data[self.currpos] = x
            self.currpos = (self.currpos+1) % self.bufsize
        def get(self):
            """ Return list of elements in correct order. """
            return self.data[self.currpos:]+self.data[:self.currpos]

    def add(self,x):
        """ Add an element at the end of the buffer"""
        self.data.append(x)
        if len(self.data) == self.bufsize:
            # Initializing current position attribute
            self.currpos = 0
            # Permanently change self's class from not-yet-full to full
            self.__class__ = self.__Full

    def get(self):
        """ Return a list of elements from the oldest to the newest. """
        return self.data


# Sample usage to recreate example figure values
import numpy as np
if __name__ == '__main__':

    # Creating ring buffer
    x = RingBuffer(10)
    # Adding first 4 elements
    x.add(5); x.add(10); x.add(4); x.add(7)
    # Displaying class info and buffer data
    print(x.__class__, x.get())

    # Creating fictitious sampling data list
    data = [1, 11, 6, 8, 9, 3, 12, 2]

    # Adding elements until buffer is full
    for value in data[:6]:
        x.add(value)
    # Displaying class info and buffer data
    print(x.__class__, x.get())

    # Adding data simulating a data acquisition scenario
    print('')
    print('Mean value = {:0.1f}   |  '.format(np.mean(x.get())), x.get())
    for value in data[6:]:
        x.add(value)
        print('Mean value = {:0.1f}   |  '.format(np.mean(x.get())), x.get())

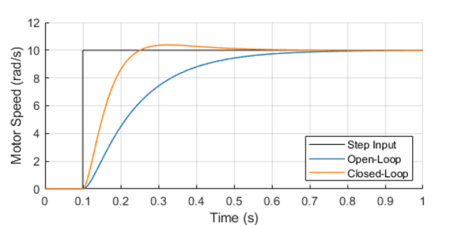
The output shown next is produced if the code containing the class is executed. The values and the states of the ring buffer shown in the figures at the beginning of the post are recreated in an iterative process that simulates some data acquisition. Note how the ring buffer class changes once the buffer is full.

    <class '__main__.RingBuffer'> [5, 10, 4, 7]
    <class '__main__.RingBuffer.__Full'> [5, 10, 4, 7, 1, 11, 6, 8, 9, 3]

    Mean value = 6.4   |   [5, 10, 4, 7, 1, 11, 6, 8, 9, 3]
    Mean value = 7.1   |   [10, 4, 7, 1, 11, 6, 8, 9, 3, 12]
    Mean value = 6.3   |   [4, 7, 1, 11, 6, 8, 9, 3, 12, 2]

As a final remark, in the Pulse Rate Monitor post, the buffer that was used is not a true circular buffer, since the elements in the arrays are shifted by one position for every new value being sampled. Because the buffer is relatively small (200 elements) and the sampling period of the data is reasonably large (0.1s) this solution does not constitute a problem. You can check out the code that implements a true ring buffer for the monitor on my GitHub page.

LED Dimmer with Raspberry Pi

LED Dimmer with Raspberry Pi

In this simple hardware setup, we will explore different coding possibilities using a Raspberry Pi with only a push button and an LED. It will be a good opportunity to compare Python classes vs functions, with code that shows the benefits of the former. More specifically, classes offer modularity and the possibility of reuse through multiple instances.

The diagram shows the very straightforward setup where the button and LED have one of their legs connected to a (distinct) GPIO pin and the other to a ground pin. A 330 Ω resistor must be connected in series with the LED, whose intensity is controlled by a PWM output. That is as simple as it gets.

Note: If the button doesn’t seem to be working, try connecting a different pair of legs, since some of them could be common.

While the dimmer functionality could be achieved using solely electronic circuitry and without a Raspberry Pi, the main point of this post is to explore coding and see what can be done with software!

Let’s start with the requirements of how we want the dimmer to work. By pressing and holding the button, the LED light intensity should increase linearly until reaching its maximum value and then decrease until it reaches its minimum value (LED off). This cycle repeats itself until the button is released, causing the light intensity to stay constant at its last value. By pressing the button again, the cycle resumes from where it stopped.

The plots provide a visual understanding of the requirements. The PWM output controlling the LED intensity ramps up (green) and down (red) while the button is pressed. As it is released, the last PWM output level is then held until the button is pressed again.

In terms of control logic, I use an integer to count ramp transitions. Even values correspond to upward ramps and odd values to downward ramps. Every time the button is released and then pressed again, the counter is reset to zero.

There are two main components in the control logic for the dimmer:

  • The calc_ramp() function that creates the triangular wave output in three steps. 1) Linear output generation, 2) Converting linear output to a tooth saw wave, thus limiting it between 0 and 1, and 3) Flipping odd count sections to generate a triangular wave.
  • Time shifting and counter reset to ensure smooth transitions every time the button is released and then pressed again. When a ramp is interrupted due to a button release event, it it will restart from where it stopped so the effective ramp duration (discounting the elapsed released time) is always the same.

Python Function

The code below shows how the function calc_ramp() and the time shifting are integrated inside an execution loop that controls the LED light intensity. As usual, the interface with the Raspberry Pi is done using GPIO Zero classes, more specifically DigitalInputDevice for the button pin and PWMOutputDevice for the LED pin.

# Importing modules and classes
import time
import numpy as np
from gpiozero import DigitalInputDevice, PWMOutputDevice
from utils import plot_line

# Assigning dimmer parameter values
pinled = 17  # PWM output (LED input) pin
pinbutton = 5  # button input pin
pwmfreq = 200  # PWM frequency (Hz)
pressedbefore = False  # Previous button pressed state
valueprev = 0  # Previous PWM value
kprev = 0  # Previous PWM ramp segmment counter
tshift = 0  # PWM ramp time shift (to start where it left off)
tramp = 2  # PWM output 0 to 100% ramp time (s)
# Assigning execution loop parameter values
tsample = 0.02  # Sampling period for code execution (s)
tstop = 30  # Total execution time (s)

# Preallocating output arrays for plotting
t = [] # Time (s)
value = [] # PWM output duty cycle value
k = [] # Ramp segment counter


def calc_ramp(t, tramp):
    """
    Creates triangular wave output with amplitude 0 to 1 and period 2 x tramp.

    """
    # Creating linear output so the value is 1 when t=tramp
    valuelin = t/tramp
    # Creating time segment counter
    k = t//tramp
    # Shifting output down by number of segment counts
    value = valuelin - k
    # Flipping odd count output to create triangular wave
    if (k % 2) == 1:
        value = 1 - value
    return value, k


# Creating button and PWM output (LED input) objects
button = DigitalInputDevice(pinbutton, pull_up=True, bounce_time=0.1)
led = PWMOutputDevice(pinled, frequency=pwmfreq)

# Initializing timers and starting main clock
tpressed = 0
tprev = 0
tcurr = 0
tstart = time.perf_counter()
# Initializing PWM value and ramp time segment counter
valuecurr = 0
kcurr = -1

# Executing loop
print('Running code for', tstop, 'seconds ...')
while tcurr <= tstop:
    # Executing code every `tsample` seconds
    if (np.floor(tcurr/tsample) - np.floor(tprev/tsample)) == 1:
        # Getting button properties only once
        pressed = button.is_active
        # Checking for button press
        if pressed and not pressedbefore:
            # Calculating ramp time shift based on last PWM value
            if (kprev % 2) == 0:
                tshift = valueprev*tramp
            else:
                tshift = (1-valueprev)*tramp + tramp
            # Starting pressed button timer
            tpressed = time.perf_counter() - tstart
            # Updating previous button state
            pressedbefore = True
        # Checking for button release
        if not pressed and pressedbefore:
            # Storing PWM value and ramp segment counter
            valueprev = led.value
            kprev = kcurr
            # Updating previous button state
            pressedbefore = False
        # Updating PWM output (LED intensity)
        if pressed:
            valuecurr, kcurr = calc_ramp(tcurr-tpressed+tshift, tramp)
            led.value = valuecurr
        # Appending current values to output arrays
        t.append(tcurr)
        value.append(valuecurr)
        k.append(kcurr)
    # Updating previous time and getting new current time (s)
    tprev = tcurr
    tcurr = time.perf_counter() - tstart
print('Done.')
# Releasing pins
led.close()
button.close()

# Plotting results
plot_line([t]*2, [value, k],
        yname=['PWM Output', 'Segment Counter'], axes='multi')
plot_line([t[1::]], [1000*np.diff(t)], yname=['Sampling Period (ms)'])

Python Class

Having the function and the time shifting “mixed” with the code makes for a less clean execution loop section, which can get pretty busy if there are more devices being controlled inside of it. The next piece of code shows how to integrate the two main components of the dimmer control inside a Python class. In addition to removing complexity from the execution loop, it makes it really easy to run multiple dimmers at the same time! This circles back to the modularity that was mentioned at the top of the post. You can create different classes for more complex devices and have them all be part of a module, such as gpiozero_extended.py. In the example below, I create two LED dimmer objects that can be controlled independently.

# Importing modules and classes
import time
import numpy as np
from gpiozero import DigitalInputDevice, PWMOutputDevice


class Dimmer:
    """
    Class that represents an LED dimmer.

    """
    def __init__(self, pinbutton=None, pinled=None):
        # Assigning GPIO pins
        self._pinbutton = pinbutton  # button input pin
        self._pinled = pinled  # PWM output (LED input) pin
        # Assigning dimmer parameter values
        self._pwmfreq = 200  # PWM frequency (Hz)
        self._tshift = 0  # PWM ramp time shift (to start where it left off)
        self._tramp = 2  # PWM output 0 to 100% ramp time (s)
        self._tpressed = 0  # Time button was pressed (s)
        self._tstart = 0  # Starting time of dimmer execution
        self._pressed = False  # Current button pressed state
        self._pressedbefore = False  # Previous button pressed state
        self._valueprev = 0  # Previous PWM value
        self._kcurr = -1  # Current PWM ramp segment counter
        self._kprev = 0  # Previous PWM ramp segmment counter
        # Creating button and PWM output (LED input) objects
        self._button = DigitalInputDevice(self._pinbutton, pull_up=True, bounce_time=0.1)
        self._led = PWMOutputDevice(self._pinled, frequency=self._pwmfreq)

    def _calc_ramp_value(self, t):
        # Creating linear output so the value is 1 when t=tramp
        valuelin = t/self._tramp
        # Creating time segment counter
        self._kcurr = t//self._tramp
        # Shifting output down by number of segment counts
        value = valuelin - self._kcurr
        # Flipping odd count output to create triangular wave
        if (self._kcurr % 2) == 1:
            value = 1 - value
        return value

    def reset_timer(self, tstart):
        # Resets dimmer timer to `tstart`
        self._tstart = tstart

    def update_value(self, t):
        # Getting button properties only once
        self._pressed = self._button.is_active
        # Checking for button press
        if self._pressed and not self._pressedbefore:
            # Calculating ramp time shift based on last PWM value
            if (self._kprev % 2) == 0:
                self._tshift = self._valueprev*self._tramp
            else:
                self._tshift = (1-self._valueprev)*self._tramp + self._tramp
            # Starting pressed button timer
            self._tpressed = time.perf_counter() - self._tstart
            # Updating previous button state
            self._pressedbefore = True
        # Checking for button release
        if not self._pressed and self._pressedbefore:
            # Storing PWM value and ramp segment counter
            self._valueprev = self._led.value
            self._kprev = self._kcurr
            # Updating previous button state
            self._pressedbefore = False
        # Updating PWM output (LED intensity)
        if self._pressed:
            self._led.value = self._calc_ramp_value(t-self._tpressed+self._tshift)

    def __del__(self):
        self._button.close()
        self._led.close()


# Assigning execution loop parameter values
tsample = 0.02 # Sampling period for code execution (s)
tstop = 30 # Total execution time (s)

# Creating dimmer objects
dimmer1 = Dimmer(pinled=17, pinbutton=5)
dimmer2 = Dimmer(pinled=18, pinbutton=6)

# Initializing timers and starting main clock
tprev = 0
tcurr = 0
tstart = time.perf_counter()
# Resettting dimmer timer
dimmer1.reset_timer(tstart)
dimmer2.reset_timer(tstart)

# Executing loop
print('Running code for', tstop, 'seconds ...')
while tcurr <= tstop:
    # Executing code every `tsample` seconds
    if (np.floor(tcurr/tsample) - np.floor(tprev/tsample)) == 1:
        # Updating dimmer outputs
        dimmer1.update_value(tcurr)
        dimmer2.update_value(tcurr)
    # Updating previous time and getting new current time (s)
    tprev = tcurr
    tcurr = time.perf_counter() - tstart
print('Done.')

# Releasing pins
del dimmer1
del dimmer2

If you watch the video, you’ll notice that the light intensity change is not as linear as one would expect, even when the PWM output is. One way to improve this is to add a non-linear transfer function between the ramp function output and the actual PWM set point value.

Also, it would be nice to have the ability to switch the dimmer off by, for instance, pressing and releasing the button for a short period of time. The improved class that does that can be found on my GitHub page.

Ultrasonic Sensor with Raspberry Pi

Ultrasonic Sensor with Raspberry Pi

An ultrasonic sensor can be used to detect the distance to an obstacle placed in front of it. The HC-SR04 sensor is an affordable option with fairly good accuracy for measurements between a couple of centimeters and a couple of meters. While primarily designed to work with an Arduino, this type of ultrasonic sensor can easily be used with a Raspberry Pi, provided some adjustments to the level of the signal voltage are made.

The wiring schematic above illustrates how to connect the ultrasonic sensor to the Pi. The HC-SR04 works with 5V for the supply voltage as well as for the logic signals Trig (emits ultrasonic sound wave) and Echo (detects reflected sound wave). Since the Raspberry Pi GPIO pins work with 3.3V logic signals, a voltage divider must be used. A 1:2 ratio of the resistors, as shown in the diagram, will do the trick. In my case I used 1 and 2 kΩ respectively. The Trig and (divided) Echo signals can then be connected to any Pi GPIO pins.

Operating principle of the HC-SR04

As mentioned earlier, this ultrasonic sensor has two logic pins that are used to detect the presence of an object:

  • Trigger – When activated by a 10 μs pulse, it emits an 8-pulse train of ultrasonic sound (40 kHz). The 8-pulse pattern is designed to help the receiver better distinguish between the actual signal and ultrasonic ambient noise.
  • Echo – Is used to detect the reflected 8-pulse signal. It transitions from a LOW to a HIGH state as soon as the 8-pulse train is emitted. It remains HIGH until a reflected signal is detected or 38 ms are elapsed (whichever occurs first).

The distance to the obstacle can be determined by measuring the time that the Echo pin remains HIGH, and by knowing that the speed of sound is 343 m/s (at 20 degrees Celsius). The three quantities are related through the equation below, which can be solved for distance. Note that since the sound wave travels to and from the detected obstacle before it gets to the sensor receiver, a factor of 2 appears in front of the distance.

Therefore:

Remember that the Echo signal remains high for about 38 ms. Hence, by using the formula above, an object that is more that about 6.5 m away cannot be accurately detected. In practical terms, the further away the obstacle is, the easier it is for the sensor to get confused with other reflections of the emitted ultrasonic pulse train. If the space that you are trying to navigate is full of hard surfaces at varying relative angles among them (such as a maze), there will be a lot of reflected signals coming from all over! You might stand a chance to be successful if the obstacles are no more than 0.5 m away.

Sensor Interface with Python

The code below shows a very simple class that represents the ultrasonic sensor. By inspecting the code, one should be able to identify the logic to generate the Trigger signal as well as the logic to determine the time that the Echo signal remains HIGH. The formula above is also implemented in the code to calculate the distance to an obstacle.

# Importing modules and classes
import time
from gpiozero import DigitalInputDevice, DigitalOutputDevice

# Defining sensor class
class UltraSonic:
    """
    Simple class that illustrates the ultrasonic sensor operating principle.

    """
    def __init__(self, echo, trigger):
        # Assingning ultrasonic sensor echo and trigger GPIO pins
        self._usoundecho = DigitalInputDevice(echo)
        self._usoundtrig = DigitalOutputDevice(trigger)
        # Assigning speed of sound (cm/s)
        self.speedofsound = 34300

    @property
    def distance(self):
        # Sending trigger pulse (~10 us)
        self._usoundtrig.on()
        time.sleep(0.000010)
        self._usoundtrig.off()
        # Detecting echo pulse start
        while self._usoundecho.value == 0:
            trise = time.perf_counter()
        # Detecting echo pulse end
        while self._usoundecho.value == 1:
            tfall = time.perf_counter()
        # Returning distance (cm)
        return 0.5 * (tfall-trise) * self.speedofsound

    @distance.setter
    def distance(self, _):
        print('"distance" is a read only attribute.')

    def __del__(self):
        self._usoundecho.close()
        self._usoundtrig.close()


# Assigning some parameters
tsample = 1  # Sampling period for code execution (s)
tstop = 10  # Total execution time (s)
# Creating ultrasonic sensor object
usensor = UltraSonic(echo=27, trigger=4)
# Initializing variable and starting main clock
tcurr = 0
tstart = time.perf_counter()

# Execution loop
print('Running code for', tstop, 'seconds ...')
while tcurr <= tstop:
    print('Waiting for sensor...')
    time.sleep(tsample)
    # Getting current time (s)
    tcurr = time.perf_counter() - tstart
    # Displaying measured distance
    print("Distance = {:0.1f} cm".format(usensor.distance))

print('Done.')
# Deleting sensor
del usensor

There is in fact a really good implementation of an ultrasonic sensor class in GPIO Zero. It uses multi-threading to give near instantaneous sensor distance measurements. Additionally, a moving average is used in the measurement calculation to improve the signal-to-noise ratio. The code below shows how simple it is to use the DistanceSensor class.

Observe that the execution portions of the two pieces of code are virtually the same, which illustrates the portability of classes inside a program. Finally, in the examples, I used the GPIO pins 4 and 27 for the Trigger and Echo signals, respectively.

# Importing modules and classes
import time
from gpiozero import DistanceSensor

# Assigning some parameters
tsample = 1  # Sampling period for code execution (s)
tstop = 10  # Total execution time (s)
# Creating ultrasonic sensor object
usensor = DistanceSensor(echo=27, trigger=4, max_distance=2)
# Initializing variable and starting main clock
tcurr = 0
tstart = time.perf_counter()

# Execution loop
print('Running code for', tstop, 'seconds ...')
while tcurr <= tstop:
    print('Waiting for sensor...')
    time.sleep(tsample)
    # Getting current time (s)
    tcurr = time.perf_counter() - tstart
    # Displaying measured distance (with unit conversion)
    print("Distance = {:0.1f} cm".format(100*usensor.distance))

print('Done.')
# Deleting sensor
del usensor
Digital PID Controller

Digital PID Controller

Closed-Loop PID (Proportional Integral Derivative) controllers are quite popular when it comes to regulating a dynamic system that has to follow a desired set point. When compared to other types of controllers, it has the advantage of requiring little to no knowledge about the system plant for it to be designed successfully.

Before we start, the idea of this post isn’t to go over the theory of control systems. The goal is to talk about some of the characteristics of a PID controller and how to go about implementing a discrete (or digital) one with some additional features to make it more robust. In the end, we will have a Python class that represents a PID, which can be used in an execution loop to control a process or a dynamic system.

The diagram below illustrates a closed-loop system, where all the signals are represented in the time domain. The three terms of the PID are shown separately, where the controller output valueis the sum of the individual term contributions. The regulation of the plant outputto the desired set point valueis achieved as the controller continuously brings the errorbetween the set point and the plant output to zero.

The PID gains,andcan be tuned so that the closed-loop dynamic behavior ofmeets the desired response requirements. In broad terms, the proportional term reacts directly to the current value of the error between set point and desired output. Usually, the proportional term by itself cannot bring the error to zero (since it relies on the existence of an error to produce a controller output). That’s where the integral term comes into the picture: because it takes into account the accumulated error (or the integrated error) it will compensate the smallest deviations. Over time the accumulation of the deviation will be large enough to cause a controller output. The proportional and integral terms combined can bring the error to zero (for a steady state input) for most dynamic systems.

The derivative term reacts to the rate of change of the error and can be effective for sudden set point changes, by helping reduce the response overshoot. In practical applications, using a derivative term can be tricky due to its sensitivity to noise that’s typically present in the measurement of the plant output.

As a side note, the plots throughout this post were generated using MATLAB and Simulink, where the corresponding m-files and Simulink model can be found on my GitHub page. I should emphasize that I did spend some time exploring and trying to use the Python Control Systems package. However, nothing can beat Simulink when it comes to quickly representing and simulating dynamic systems. Especially when non-linearities are being modelled. Spending $100 on that MATLAB student license might be something to think about.

One way to analyze the performance of a control system (in our case a PID controller) is by measuring the closed-loop system’s response to a step change of the set point.

Because in future posts we will be doing closed loop control of small low-budget DC motors, let’s use as a plant a somewhat fictitious motor with an integral gear box. The plot shows the closed-loop system response in contrast with the open-loop response.

The controller output (armature voltage), as well as the individual contribution of each of the PID terms, is also shown. Observe how the proportional and derivative terms go to zero as the response approaches its steady-state value, leaving the integral term in charge of keeping the errorat zero.

It’s important to mention that both the open-loop as well as the closed-loop responses end up at the same final armature voltage of 2.8 V.

For our DC motor model, the armature voltage required to produce a motor speed output of 10 rad/s without any external load is 2.8 V. In the case of the open-loop system, I use that knowledge to apply a step input of 2.8 V to the motor. On the other hand, the step input to the closed-loop system is in fact the desired speed output of 10 rad/s. The PID controller will apply whatever armature voltage is needed to follow the speed set point, even when the manufacturing variability of the motor or other sources of error are present. That’s the first takeaway that most people working with control systems are very familiar with. The second point I want to make is that the improved response time, compared to the open-loop system, can only be achieved because the controller has an excess output capability (up to 12 V in our motor model) that can be tapped into at the moment of the step change.

Without getting into stability margins, the closed-loop system can be just as fast as you want. The issue at hand becomes how much do you want to “oversize” your system so it can obtain that stellar dynamic response. Understanding you engineering requirements is key when choosing the right hardware “size” for the desired closed-loop system behavior.

Discrete PID Implementation

The most basic digital PID implementation can be obtained from taking the derivative of the controller output equation

and using backward difference (with sampling period) to approximate the derivatives. The difference equation below can be obtained by following the steps shown here.

This implementation has two notable advantages:

  • Because the previous output value is taken into account for the output calculation, the controller can be seamlessly started from an open-loop condition by assigning the current open-loop output value to the very first .
  • The PID gains,andobtained from the design of a continuous controller are still valid in its discrete representation (provided a fast enough sampling periodis used).

The graphs below show the closed-loop response of the analog plant (DC motor) as well as the corresponding output of the discrete controller for a sampling period of 0.01 and 0.005 seconds. The equivalent analog controller using the same PID gains is also shown as a reference. Although not on the graphs, the discrete PID with a sampling period of 0.001 seconds produces virtually the same response as the continuous one.

As it can be seen in the graphs, the lower sampling period caused the plant output to oscillate. Further increasingwould increase the amplitude of the oscillations, eventually making the system unstable. This well known behavior is caused by the discretization of the controller, where the plant basically behaves in an open loop fashion in between sample points. Even though this problem can be approached mathematically, tackling it using a simulation tool can provide valuable insight on the compromises between sampling period and PID gains, during the initial design of the controller.

Before we put our digital PID into a Python class, let’s go over a few features that can make the controller more robust for practical applications.

Saturation and Anti-Windup

If we were to use some very aggressive gains for our motor PID controller, the step response could be further improved as shown with the solid trace below. You’ll also notice an unpractical armature voltage spike over 60 V! In reality, the controller output will saturate at its maximum (or minimum) output capability, in our case 12 V, producing the dotted line traces instead.

Once the controller output is saturated, the integral term compensation keeps increasing in an attempt to reduce the accumulated error. By the time the controller “comes back” from the saturation state, the integral term is “wound-up”, resulting in an overshoot of the response, as it can be seen by contrasting the dotted and solid orange lines above.

By implementing anti-windup logic in the discrete controller, the overshoot caused by potential saturation can be reduced, as shown on the left.

The basic idea is to turn off the integral term of the PID (as we’ll see in the Python class at the end) every time an upper or lower saturation limit is exceeded. This is a common improvement used in digital PID controllers.

Feed-Forward and Derivative Term Filtering

Another useful improvement that can be made to our digital PID is to allow for a feed-forward signalin its implementation. The feed-forward term reduces the contribution of the controller output signal , making the system less susceptible to noise in the measurement of the plant output used to calculate the error.

While not always possible, in some special situations, we can pre-calculate the feed-forward signal as a function of time and add it to controller output as shown in the block diagram. Typical applications involve a known “control path” such as a robotic manipulator (with pre-programmed motion paths) or a vehicle’s cruise control (on a highway with known topology).

As I mentioned earlier in this post, the derivative term of the PID is quite sensitive to noise in the calculated error signal, which primarily comes from the transducers used to measure the plant output. One way to help mitigate this effect is the addition of a low-pass filter to the output of the derivative term inside the controller. Let’s use my favorite first-order digital filter, given by the difference equation below, whereis the derivative term output andis the corresponding filtered output signal.

PID Python Class

Finally, it’s time to put it all together inside a Python class. If you go through the code below, you’ll be able to identify all the components that were discussed in the previous three sections. The PID class should be instantiated before entering the execution loop, while the control method is called every time step inside the execution loop. In my next post we will use this class to control the speed of a small DC motor.

class PID:
    def __init__(self, Ts, kp, ki, kd, umax=1, umin=-1, tau=0):
        #
        self._Ts = Ts  # Sampling period (s)
        self._kp = kp  # Proportional gain
        self._ki = ki  # Integral gain
        self._kd = kd  # Derivative gain
        self._umax = umax  # Upper output saturation limit
        self._umin = umin  # Lower output saturation limit
        self._tau = tau  # Derivative term filter time constant (s)
        #
        self._eprev = [0, 0]  # Previous errors e[n-1], e[n-2]
        self._uprev = 0  # Previous controller output u[n-1]
        self._udfiltprev = 0  # Previous derivative term filtered value

    def control(self, ysp, y, uff=0):
        #
        # Calculating error e[n]
        e = ysp - y
        # Calculating proportional term
        up = self._kp * (e - self._eprev[0])
        # Calculating integral term (with anti-windup)
        ui = self._ki*self._Ts * e
        if (self._uprev+uff >= self._umax) or (self._uprev+uff <= self._umin):
            ui = 0
        # Calculating derivative term
        ud = self._kd/self._Ts * (e - 2*self._eprev[0] + self._eprev[1])
        # Filtering derivative term
        udfilt = (
            self._tau/(self._tau+self._Ts)*self._udfiltprev +
            self._Ts/(self._tau+self._Ts)*ud
        )
        # Calculating PID controller output u[n]
        u = self._uprev + up + ui + udfilt + uff
        # Updating previous time step errors e[n-1], e[n-2]
        self._eprev[1] = self._eprev[0]
        self._eprev[0] = e
        # Updating previous time step output value u[n-1]
        self._uprev = u - uff
        # Updating previous time step derivative term filtered value
        self._udfiltprev = udfilt
        # Limiting output (just to be safe)
        if u < self._umin:
            u = self._umin
        elif u > self._umax:
            u = self._umax
        # Returning controller output at current time step
        return u
Python DAC Class

Python DAC Class

Creating a class to represent a Raspberry Pi digital-to-analog converter is a good example on how to put together the concepts we have been exploring in some of the previous posts. More specifically, DAC with Raspberry Pi and Classes vs. Functions in Python. Besides a Raspberry Pi and a couple of resistors and capacitors, we need an additional DAQ device to calibrate our Pi DAC output.

In the post DAC with Raspberry Pi, we used an MCP3008 to measure (and calibrate) the DAC output. This time around I will follow my recommendation of not using the same DAQ to generate and measure the output, using instead a LabJack U3. While a LabJack is not a calibration DAQ device, it is far more accurate than a Pi, therefore moving us in the right direction when it comes to choosing a calibration device.

The setup is quite simple: On the Pi side, a GPIO pin used as PWM input to the the low-pass filter and a GND pin. On the U3 side, the RC filter output (which is our DAC output) is connected to the analog input port AIN0, while the GND port is connected to the same GND as the Pi.

The U3 is connected to a separate computer via USB and will be running a variation of the code that can be found on my GitHub page. The Python package that I made containing the LabJack U3 class can be installed from the PyPI (Python Package Index) page.

As before, the cascaded second order filter is made of two first order low-pass RC filters, where R = 1 kΩ and C = 10 μF.

Of course, if you don’t have a LabJack, a digital multimeter should do the trick and allow you to measure the DAC output in order to do its calibration. I chose to use a LabJack to gain some insight on the DAC output signal by using its 50 kHz streaming capability (and because an oscilloscope is not among my few possessions).

The next step is to layout what our DAC class should look like. You may want to put down a “skeleton” of the class, as shown below, with a brief description of what the attributes are and what the methods do. Using the reserved word pass allows for placeholders for the methods to be easily created and filled out later.

class DAC:

    def __init__(self):
        # Class constructor
        self._vref = 3.3  # Reference voltage output
        self._slope = 1  # Output transfer function slope
        self._offset = 0  # Output transfer function intercept

    def __del__(self):
        # Class destructor
        # - makes sure GPIO pins are released
        pass

    def reset_calibration(self):
        # Resets the DAC slope and offset values
        pass

    def set_calibratio(self):
        # Sets the DAC slope and offset with calibration data
        pass

    def get_calibration(self):
        # Retrieves current slope and offset values
        pass

    def set_output(self):
        # Sets the DAC output voltage to the desired value
        pass

One of the nice things about using classes is that it’s easy to add (or remove) attributes and methods as you code away. And even better, if you’re using the interactive session of VS Code, saved updates to your methods are immediately reflected in any instance of the class that is present in the session’s “workspace” (to use a MATLAB term, for those familiar with it). In other words, if you were to call that method again using dot notation, it would behave based on the latest modifications that you saved.

In the case of our example, the attributes need to hold the values of a reference voltage (Pi’s 3.3 V if you’re not using any OpAmp with your filter) and the calibration parameters which are used so the DAC can output the correct set voltage value.

from gpiozero import PWMOutputDevice


class DAC:

    def __init__(self, dacpin=12):

        # Checking for valid hardware PWM pins
        if dacpin not in [12, 13, 18, 19]:
            raise Exception('Valid GPIO pin is: 12, 13, 18, or 19')
        # Assigning attributes
        self._vref = 3.3  # Reference voltage output
        self._slope = 1  # Output transfer function slope
        self._offset = 0  # Output transfer function intercept
        # Creating PWM pin object
        self._dac = PWMOutputDevice(dacpin, frequency=700)

    def __del__(self):

        # Releasing GPIO pin
        self._dac.close()

    def reset_calibration(self):
        self._slope = 1
        self._offset = 0

    def set_calibration(self, slope, offset):
        self._slope = slope
        self._offset = offset

    def get_calibration(self):
        print('Slope = {:0.4f} , Offset = {:0.4f}'.format(
            self._slope, self._offset))

    def set_output(self, value):

        # Limiting output
        output = self._slope*value/self._vref + self._offset
        if output > 1:
            output = 1
        if output < 0:
            output = 0
        # Applying output to GPIO pin
        self._dac.value = output

As far as the methods are concerned, a constructor and a destructor, being the latter a good idea so the GPIO pin can be released once you’re done using the class instance. Also, a group of methods to deal with the DAC calibration and a single method to set the DAC output value. Notice that the attribute names start with an underscore. That’s a loose Python convention to define private properties (or methods, if I were to use the underscore as the first character of the method name), unlike other programming languages which are more rigorous about it by making you explicitly define what’s private. The general idea of private properties (or methods) is that they’re not supposed to be accessible directly by the user of the program, therefore, being accessed internally by the code.

DAC Calibration

First, we create an instance of the DAC class on GPIO pin 18: mydac = DAC(dacpin=18)

Then, the output calibration is done with two output settings (0.5 and 3.0 V) using the method: mydac.set_output(0.5) and mydac.set_output(3.0). Each time the output is read using the streaming feature of the LabJack U3, as shown on the left. The high frequency noise in the signal is quite apparent and is a most likely due to the limitations of the Raspberry Pi hardware. For the two desired outputs of 0.5 and 3.0 V, the corresponding mean actual values are 0.614 and 2.854 V. Because the system response is linear, two data points are sufficient.

The slope and offset are calculated as slope = (3.0 – 0.5) / (2.854 – 0.614) = 1.116, and offset = 0.5 – (3.0 – 0.5) / (2.854 – 0.614) x 0.614 = -0.185. The calibrated values are applied to the DAC instance using the method mydac.set_calibration(1.116, -0.185). If a new calibration has to be done, the default values of 1 and 0 can be restored by using the method mydac.reset_calibration(). As mentioned earlier, the private attributes _slope and _offset are not dealt with directly by the user but instead through different methods. Of course, in this simple example, they could be changed directly by doing mydac._slope = 1.116 and mydac._offset = -0.185. In more complex situations there might be a few good reasons to avoid direct access to an instance’s attributes.

With the calibrated DAC, the new outputs to the same settings as before (0.5 and 3.0 V) give the results on the left, where the actual mean values are 0.493 and 3.006 V, respectively.

DAC Test

Let’s put the DAC device to the test! The Python code below can be used to generate a random sequence of steps every 0.5 seconds between 0 and 3 V (every 0.5 V). The data is collected using the LabJack U3 streaming feature and plotted in the next figure. Not too bad for our poor man’s DAC.

import time
import numpy as np
from gpiozero_extended import DAC

# Assigning parameter values
tstep = 0.5  # Interval between step changes (s)
tstop = 10  # Total execution time (s)

# Creating DAC object on GPIO pin 18
mydac = DAC(dacpin=18)
mydac.set_calibration(1.116, -0.185)

# Initializing timers and starting main clock
tprev = 0
tcurr = 0
tstart = time.perf_counter()

# Running execution loop
print('Running code for', tstop, 'seconds ...')
while tcurr <= tstop:
    # Updating analog output every `tstep` seconds with
    # random voltages between 0 and 3 V every 0.5 V
    if (np.floor(tcurr/tstep) - np.floor(tprev/tstep)) == 1:
        mydac.set_output(np.round(6*np.random.rand())/2)
    # Updating previous time and getting new current time (s)
    tprev = tcurr
    tcurr = time.perf_counter() - tstart

print('Done.')
# Releasing pin
del mydac
Classes vs. Functions in Python

Classes vs. Functions in Python

Using classes (or more broadly object-oriented programming) can really take your coding to the next level. While they can be a bit confusing at first, some of the things you can do with them would be very difficult, if not impossible, to do using function-based programming. A very good and concise definition of classes in Python can be found in the official documentation, which I’ll literally quote below:

“Classes provide a means of bundling data and functionality together. Creating a new class creates a new type of object, allowing new instances of that type to be made. Each class instance can have attributes attached to it for maintaining its state. Class instances can also have methods (defined by its class) for modifying its state.”

If you’re already using functions in Python, moving to classes is a very feasible step. The approach I will take in this post is to compare a class and a set of functions that do the same thing, i.e., some data fitting. As we go over the comparison, I will also be referencing bits and pieces of the quote above, hopefully making it more clear to understand.

First of all, you will want to bundle data and functionality that actually belong together. With that in mind, using classes will actually make sense in the long run.

The attributes is where the data (or states) are kept inside an instance of the class. Because of the nature of classes, each instance exists in the computer memory completely independent of other instances of the same class. In other words, the attributes (or properties) of each instance can hold different values. All instances still contain the same methods of the class. These are actions that can be performed by a given instance that usually modify the attribute values of that particular instance.

If you use functions on a regular basis and look inside a Python class, you’ll recognize that the methods are basically functions. That set of functions that you created to perform related tasks on your data can all be put inside a class. Besides making your code more modular and self-contained, the fact that you can have multiple instances of the same class can come in really handy, as we’ll see later on. All the code in this post can be found on my GitHub page, as well.

Let’s get started on our data fitting code. The data part is a set of ordered (x, y) pairs that will be used in a linear regression. The functionality part is the set of actions that can be performed on the data. More specifically: defining the data points, fitting a line to them, and plotting the original data points and the line of best fit.

As a general grammatical recommendation, variables (or attributes) are substantives, or groups of substantives, since they contain or define something. Variable names such as figuresize, x_values, numdatapoints are all typical in Python.

Since, functions or methods “do something” with “something”, I always start with a verb and then one or more substantives. So, open_figure, define_data, find_data_points are all valid names. It is a convention in Python to use underscores in function or method names. If you use underscores in your variable names, that verb is all you got to quickly distinguish between attributes (variables) and methods (functions) in your code.

Data Fitting Functions

With that said, let’s check below the three (very simple) functions that will be used. One important aspect is that most functions have input arguments and return values. In this simple example, the functions define_data and fit_data return dictionaries containing the output information. In larger projects, functions may be calling functions, who in turn call more functions. Handling and tracking input and output can become pretty complex. By then, most people resort to global variables. Which, in my opinion, should be avoided at all costs. Having local variables that stay local to their functions will make debugging the code much more straightforward.

import numpy as np
import plotly.graph_objects as go
from scipy.stats import linregress


def define_data(x, y, xname=None, yname=None):
    """
    Creates dictionary containing data information.

    """
    if len(x) == len(y):
        data = {
            'xname': xname,
            'yname': yname,
            'x': x,
            'y': y,
        }
    else:
        raise Exception("'x' and 'y' must have the same length.")
    return data


def fit_data(data):
    """
    Calculates linear regression to data points.

    """
    f = linregress(data['x'], data['y'])
    fit = {
        'slope': f.slope,
        'intercept': f.intercept,
        'r2': f.rvalue**2
    }
    print('Slope = {:1.3f}'.format(fit['slope']))
    print('Intercept = {:1.3f}'.format(fit['intercept']))
    print('R-squared = {:1.3f}'.format(fit['r2']))
    return fit


def plot_data(data, fit):
    """
    Creates scatter plot of data and best fit regression line.

    """
    # Making sure x and y values are numpy arrays
    x = np.array(data['x'])
    y = np.array(data['y'])
    # Creating plotly figure
    fig = go.Figure()
    # Adding data points
    fig.add_trace(
        go.Scatter(
            name='data',
            x=x,
            y=y,
            mode='markers',
            marker=dict(size=10, color='#FF0F0E')
        )
    )
    # Adding regression line
    fig.add_trace(
        go.Scatter(
            name='fit',
            x=x,
            y=fit['slope']*x+fit['intercept'],
            mode='lines',
            line=dict(dash='dot', color='#202020')
        )
    )
    # Adding other figure objects
    fig.update_xaxes(title_text=data['xname'])
    fig.update_yaxes(title_text=data['yname'])
    fig.update_layout(
        paper_bgcolor='#F8F8F8',
        plot_bgcolor='#FFFFFF',
        width=600, height=300,
        margin=dict(l=60, r=30, t=30, b=30),
        showlegend=False)
    fig.show()

Below is a little program that uses the three functions to fit some x, y values. Notice how inputs and outputs have to be passed around between functions. Also, if we want to fit a different set of data points, we start carrying around multiple variables in memory, which can eventually be overwritten or confused with something else. By the way, I’m assuming you saved a file named fitfunctons.py in a modules folder which is either on the Python path or is your current working folder.

from modules.fitfunctions import define_data, fit_data, plot_data

# Defining first data set
x1 = [0, 1, 2, 3, 4]
y1 = [2.1, 2.8, 4.2, 4.9, 5.1]
data1 = define_data(x1, y1, xname='x1', yname='y1')
# Fitting data
fit1 = fit_data(data1)
# Plotting results
plot_data(data1, fit1)

# Defining second data set
x2 = [0, 1, 2, 3, 4]
y2 = [3, 5.1, 6.8, 8.9, 11.2]
data2 = define_data(x2, y2, xname='x2', yname='y2')
# Fitting data
fit2 = fit_data(data2)
# Plotting results
plot_data(data2, fit2)

Data Fitting Class

Now let’s take a look at a class (saved in fitclass.py in the same modules folder) that contains the three functions as methods. As far as naming conventions in Python are concerned, classes use UpperCamelCase. Therefore, our class will be called FitData. In addition to the three functions (now as methods inside the class) there’s a constructor method, which is by convention named __init__. It’s in the constructor that we can initialize attributes, in this case the data and fit dictionaries, as well as call other methods. Notice that the first argument to all methods is self, which will hold the pointer to the class instance once that instance is created, and is how attributes and methods are accessed inside the class.

For instance, by passing only self to the fit_data method, I can access any attribute or method of the class by using the self argument with dot notation. For instance, self.data['x'] gets the x values array anytime I need it inside the class.

On the same token, methods don’t need to have return values (although sometimes you may want them to). They can use the self pointer to store the return values as a class attribute. The method fit_data gets the x, y values from the data attribute and stores the fitting parameters in the fit attribute, such as self.fit['slope'] = f.slope. 

import numpy as np
import plotly.graph_objects as go
from scipy.stats import linregress


class FitData:
    def __init__(self):
        """
        Class constructor.

        """
        self.data = dict()
        self.fit = dict()

    def define_data(self, x, y, xname=None, yname=None):
        """
        Creates dictionary containing data information.

        """
        if len(x) == len(y):
            self.data['x'] = x
            self.data['y'] = y
            self.data['xname'] = xname
            self.data['yname'] = yname
        else:
            raise Exception("'x' and 'y' must have the same length.")

    def fit_data(self):
        """
        Calculates linear regression to data points.

        """
        f = linregress(self.data['x'], self.data['y'])
        self.fit['slope'] = f.slope
        self.fit['intercept'] = f.intercept
        self.fit['r2'] = f.rvalue**2
        print('Slope = {:1.3f}'.format(self.fit['slope']))
        print('Intercept = {:1.3f}'.format(self.fit['intercept']))
        print('R-squared = {:1.3f}'.format(self.fit['r2']))

    def plot_data(self):
        """
        Creates scatter plot of data and best fit regression line.

        """
        # Making sure x and y values are numpy arrays
        x = np.array(self.data['x'])
        y = np.array(self.data['y'])
        # Creating plotly figure
        fig = go.Figure()
        # Adding data points
        fig.add_trace(
            go.Scatter(
                name='data',
                x=x,
                y=y,
                mode='markers',
                marker=dict(size=10, color='#FF0F0E')
            )
        )
        # Adding regression line
        fig.add_trace(
            go.Scatter(
                name='fit',
                x=x,
                y=self.fit['slope']*x+self.fit['intercept'],
                mode='lines',
                line=dict(dash='dot', color='#202020')
            )
        )
        # Adding other figure objects
        fig.update_xaxes(title_text=self.data['xname'])
        fig.update_yaxes(title_text=self.data['yname'])
        fig.update_layout(
            paper_bgcolor='#F8F8F8',
            plot_bgcolor='#FFFFFF',
            width=600, height=300,
            margin=dict(l=60, r=30, t=30, b=30),
            showlegend=False
        )
        fig.show()

The program below can be contrasted with the one that employed the functions. We can start by creating two instances of the FitData class, which will be two distinct and independent objects in the computer memory. Each instance now holds the self pointer and can therefore access attributes and call methods using dot notation. fitdata1.plot_data() will run that method with whatever attributes are required and that are already stored in that particular instance. Also, print(fitdata2.data) would display the values assigned to the data attribute in the fitdata2 object.

from modules.fitclass import FitData

# Creating class instances
fitdata1 = FitData()
fitdata2 = FitData()

# Defining first data set
x1 = [0, 1, 2, 3, 4]
y1 = [2.1, 2.8, 4.2, 4.9, 5.1]
fitdata1.define_data(x1, y1, xname='x1', yname='y1')
# Fitting data
fitdata1.fit_data()
# Plotting results
fitdata1.plot_data()

# Defining second data set
x2 = [0, 1, 2, 3, 4]
y2 = [3, 5.1, 6.8, 8.9, 11.2]
fitdata2.define_data(x2, y2, xname='x2', yname='y2')
# Fitting data
fitdata2.fit_data()
# Plotting results
fitdata2.plot_data()

You should also observe that all the variables that were being passed around are now incapsulated inside each object, making for code that is more organized and less prone to errors. Of course, these examples are quite simple and keeping track of what’s going on is still pretty straightforward.

Finally, similar to functions, methods can call methods. But since input arguments and return values can all be stored inside the class attributes, nesting method calls becomes much cleaner and easier to do than nesting function calls.

Random Remarks

I was first exposed to Object-Oriented Programming a little over 6 years ago, when I was playing around with a LEGO EV3 Mindstorms. It was in MATLAB, which was my programming language of many, many years. It took me some time to wrap my head around the concept, but once I understood its power, a whole new dimension of programming opened up! I then took to write the code for an entire engine test cell automation system: GUIs, instrumentation interfaces, and everything in between. The level of complexity and modularization that was required in order to succeed was only achievable through the use of classes.

Speaking of GUIs, those are built upon the concept of classes. If you ever venture down that path, there’s another strong reason to learn more and start using them. Once you get it, you’ll never look back.