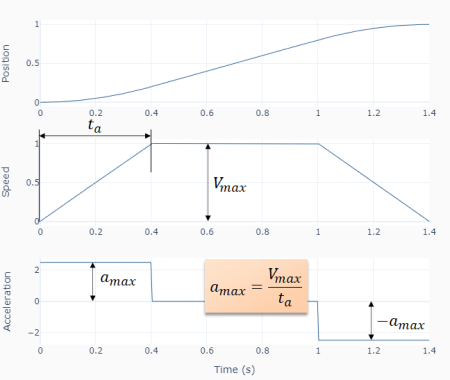
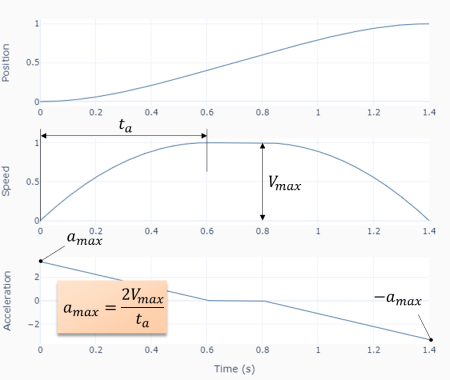
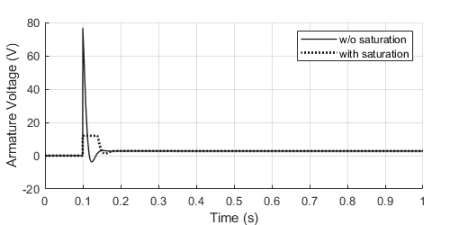
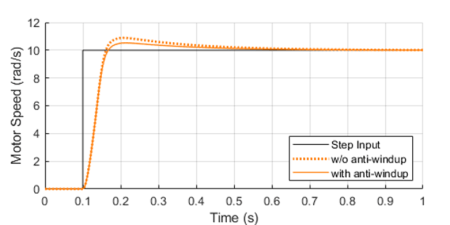
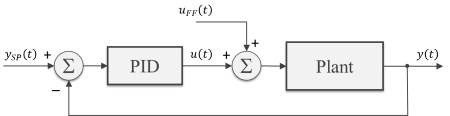
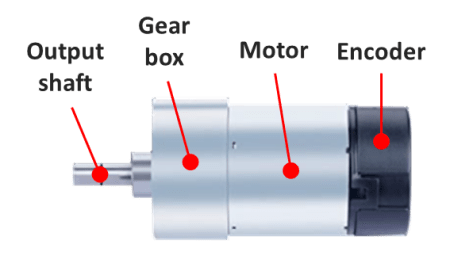
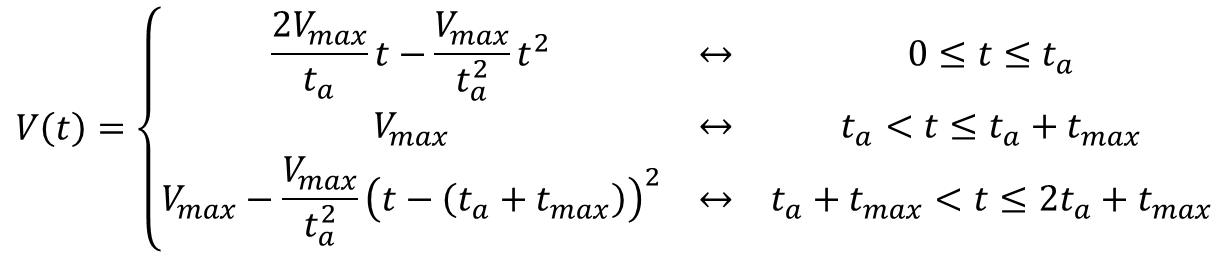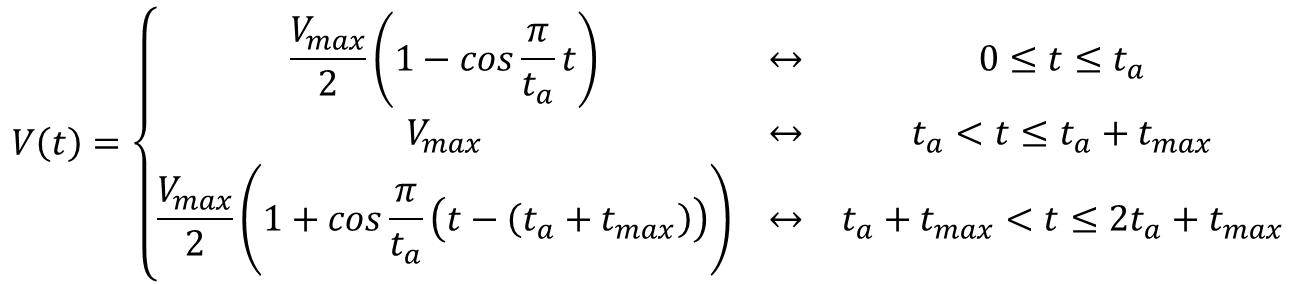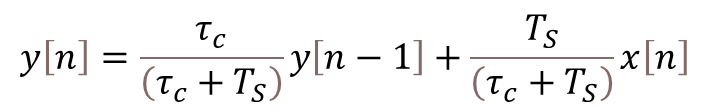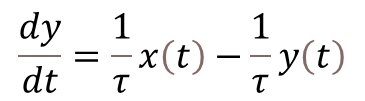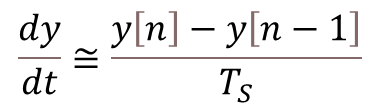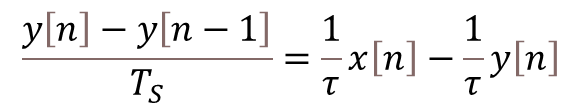These types of LED displays are quite popular and can be used to add a visual output to a Raspberry Pi automation project. In this post, I will be talking about the KS0445 4-digit LED Display Module from keyestudio. While keyestudio kits are primarily designed to work with Arduino, they are perfectly suitable for Pi applications.
In theory, any LED 4-digit Display using a TM1637 chip can be used with the Python code that will be shown.
The first step is to install the TM1637 Python package containing the class that will simplify controlling the LED display quite a bit. As a side note, I strongly encourage installing VS Code on the Pi, so you can code like a pro.
Open a terminal window in VS Code and type:
pip install raspberrypi-tm1637
Once the installation is complete, you can wire the display as shown below and try the Python code that follows. It illustrates how straightforward it is to use some of the methods of the TM1637 class that come in the package.
# Importing modules and classes
import tm1637
import time
import numpy as np
from datetime import datetime
from gpiozero import CPUTemperature
# Creating 4-digit 7-segment display object
tm = tm1637.TM1637(clk=18, dio=17) # Using GPIO pins 18 and 17
clear = [0, 0, 0, 0] # Defining values used to clear the display
# Displaying a rolling string
tm.write(clear)
time.sleep(1)
s = 'This is pretty cool'
tm.scroll(s, delay=250)
time.sleep(2)
# Displaying CPU temperautre
tm.write(clear)
time.sleep(1)
cpu = CPUTemperature()
tm.temperature(int(np.round(cpu.temperature)))
time.sleep(2)
# Displaying current time
tm.write(clear)
time.sleep(1)
now = datetime.now()
hh = int(datetime.strftime(now,'%H'))
mm = int(datetime.strftime(now,'%M'))
tm.numbers(hh, mm, colon=True)
time.sleep(2)
tm.write(clear)
Raspberry Pi Stopwatch with LED Display
That was pretty much it for the LED display. However, let’s go for an Easter egg, where we implement a stopwatch that can be controlled by keyboard inputs. The main feature here is the use of the Python pynput package, which seamlessly enables non-blocking keyboard inputs. To get started, in a terminal window in VS Code, type:
pip install pynput
To make things more interesting, I created the class StopWatch with the following highlights:
- First and foremost, could the entire code be written using a function (or a few functions) or even as a simple script? Yes, it could. However, using a class makes for code that is much more modular and expandable, and that can easily be integrated into other code.
- At the center of the the StopWatch class is the execution loop method. For conciseness and readability, all other methods (with very descriptive names) are called from within this execution loop.
- The beauty of using a class and therefore its methods is that the latter can be called from different points in the code, as it is the case of the
start_watch()method, for example. - Finally, as the code is written as a class vs. functions, all the variables can be defined as class attributes. That really reduces complexity with input arguments, if functions were to be used instead.
# Importing modules and classes
import time
import tm1637
import numpy as np
from pynput import keyboard
class StopWatch:
"""
The class to represent a digital stopwatch.
**StopWatch** runs on a Raspberry PI and uses a 4-digit 7-segment display
with a TM1637 control chip.
The following keyboard keys are used:
* ``'s'`` to start/stop the timer.
* ``'r'`` to reset the timer.
* ``'q'`` to quit the application.
"""
def __init__(self):
"""
Class constructor.
"""
# Creating 4-digit 7-segment display object
self.tm = tm1637.TM1637(clk=18, dio=17) # Using GPIO pins 18 and 17
self.tm.show('00 0') # Initializing stopwatch display
# Creating keyboard event listener object
self.myevent = keyboard.Events()
self.myevent.start()
# Defining time control variables (in seconds)
self.treset = 60 # Time at which timer resets
self.ts = 0.02 # Execution loop time step
self.tdisp = 0.1 # Display update period
self.tstart = 0 # Start time
self.tstop = 0 # Stop time
self.tcurr = 0 # Current time
self.tprev = 0 # Previous time
# Defining execution flow control flags
self.run = False # Timer run flag
self.quit = False # Application quit flag
# Running execution loop
self.runExecutionLoop()
def runExecutionLoop(self):
"""
Run the execution loop for the stopwatch.
"""
# Running until quit request is received
while not self.quit:
# Pausing to make CPU life easier
time.sleep(self.ts)
# Updating current time value
self.update_time()
# Handling keyboard events
self.handle_event()
# Checking if automatic reset time was reached
if self.tcurr >= self.treset:
self.stop_watch()
self.reset_watch()
self.start_watch()
# Updating digital display
self.update_display()
# Stroing previous time step
self.tprev = self.tcurr
def handle_event(self):
"""
Handle non-blocking keyboard inputs that control stopwatch.
"""
# Getting keyboard event
event = self.myevent.get(0.0)
if event is not None:
# Checking for timer start/stop
if event.key == keyboard.KeyCode.from_char('s'):
if type(event) == keyboard.Events.Release:
if not self.run:
self.run = True
self.start_watch()
elif self.run:
self.run = False
self.stop_watch()
# Checking for timer reset
elif event.key == keyboard.KeyCode.from_char('r'):
if type(event) == keyboard.Events.Release:
if not self.run:
self.reset_watch()
elif self.run:
print('Stop watch before resetting.')
# Checking for application quit
elif event.key == keyboard.KeyCode.from_char('q'):
self.quit = True
self.tm.write([0, 0, 0, 0])
print('Good bye.')
def start_watch(self):
""" Update start time. """
self.tstart = time.perf_counter()
def stop_watch(self):
""" Update stop time. """
self.tstop = self.tcurr
def reset_watch(self):
""" Reset timer. """
self.tstop = 0
self.tm.show('00 0')
def update_time(self):
""" Update timer value. """
if self.run:
self.tcurr = time.perf_counter() - self.tstart + self.tstop
def update_display(self):
""" Update digital display every 'tdisp' seconds. """
if (np.floor(self.tcurr/self.tdisp) - np.floor(self.tprev/self.tdisp)) == 1:
# Creating timer display string parts (seconds, tenths of a second)
if int(self.tcurr) < 10:
tsec = '0' + str(int(self.tcurr))
else:
tsec = str(int(self.tcurr))
ttenth = str(int(np.round(10*(self.tcurr-int(self.tcurr)))))
# Showing string on digital display
self.tm.show(tsec + ' ' + ttenth)
# Running instance of StopWatch class
if __name__ == "__main__":
StopWatch()
and
(shown in the diagram on the left), as well as other parameters that define the trajectory, are known before the position tracking is executed.
(at the beginning and end of the motion) and the maximum allowed velocity
as the additional parameters that are sufficient to fully determine the path.
at maximum speed is given by:
.
can be used interchangeably, where, in this case, 
. The Python function below shows one possible implementation of the path calculation, where the position and acceleration traces are calculated through numerical integration and derivative, respectively. I found this approach to be more robust to the path discretization, specially at the speed profile transitions.
is the sum of the individual term contributions. The regulation of the plant output
to the desired set point value
is achieved as the controller continuously brings the error
between the set point and the plant output to zero.
,
and
can be tuned so that the closed-loop dynamic behavior of
) to approximate the derivatives. The difference equation below can be obtained by following the steps shown 
is taken into account for the output calculation, the controller can be seamlessly started from an open-loop condition by assigning the current open-loop output value to the very first 
in its implementation. The feed-forward term reduces the contribution of the controller output signal 
is the derivative term output and
is the corresponding filtered output signal.
. Also, for simplicity, consider a first order filter which, in terms of difference equations, only depends on the values of the current and last time steps, or 
and 
. Thus:
, 
and
. Luckily for us, the 
is given by 
, where
is the response time of the filter and is related to the filter cutoff frequency
by:
.
using backward difference (with sampling period
and
into their discrete counterparts
in this particular case).
and the current input value
), the faster the filter is (higher cutoff frequency) and the more it follows the input value. Conversely, the slower the filter (
), the more the output takes into account the previous value.
below, and type python in the search bar. Several extensions will show up. Select the Python (Pylance) extension and 
and install it.
. Sometimes it’s installed automatically when you install the previous extension.
and then select 
Python as the programming language.
Things DAQ 